By Francesco Ardizzon, Nicola Laurenti, Carlo Sarto and Giovanni Gamba
To ensure the authenticity of the Galileo navigation messages, the Open Service navigation message authentication (OSNMA) mechanism requires a loose synchronization between the receiver clock and the system time.
To ensure the authenticity and the integrity of the transmitted messages, the Timed Efficient Stream Loss-tolerant Authentication (TESLA) protocol for broadcast authentication requires a loose time synchronization between the transmitter and the receiver — that is, an upper bound to the time offset between their clocks. In the context of the TESLA-based Open Service navigation message authentication (OSNMA) protocol, it is customary to assume that:
- On the system side, the transmission is synchronous because the satellites are equipped with high-precision atomic clocks, the drift of which is assumed negligible with respect to those at the receiver side.
- At the receiver side, commercial clocks can be found that are less accurate and less stable, which accounts for the substantial time mismatch between the transmitter and the receiver clocks accumulating over time.
To limit the impact of such mismatch on OSNMA operation, it is envisioned that clocks for authenticated tachographs onboard vehicles, such as the ones that will be employed for the position authenticated tachograph for OSNMA launch (PATROL) project, are reset and precisely realigned to system time in periodic workshop visits. However, the clock mismatch must satisfy the OSNMA constraint at all times between successive workshop resets, in the “holdover” period, and through all possible operating conditions, to ensure constant authenticity of the navigation message.
In other contexts, this task is performed by such means as network synchronization protocols.
However, we are considering a scenario where, during holdover, we cannot rely on other sources, such as an internet connection or other devices to synchronize with the reference time to assure the authenticity of our time reference and, consequently, of the PVT solution. We also cannot trust any signal received during the holdover period, thus we should not use the PVT solution to synchronize the clock.
Here, we have two goals. First, investigate the causes of the misalignment and frequency deviation in clock generators commonly found on the market for GNSS receivers. Second, relate the clock specification parameters, taken directly from the real-time clock (RTC) device datasheets, the holdover period, and the OSNMA misalignment constraints.

Atomic clocks at ESTEC’s Navigation Laboratory in The Netherlands independently validate Galileo timing performance. (Photo: ESA)
Frequency Accuracy and Stability
Two metrics are usually employed to evaluate the performance of an oscillator.
- Clock frequency accuracy is the normalized difference between the frequency output and its nominal value, f0.
- Clock frequency stability is the normalized instantaneous frequency deviation from its local mean.
Although devices are characterized in terms of their stability, we are interested in measuring their accuracy y(t)ΔF(t)⁄f0, where ΔF(t) is the instantaneous frequency deviation from f0 at time t. The calibration performed during each workshop reset brings the residual misalignment to a negligible value called phase calibration error. On the other hand, we will later discuss the residual frequency deviation, due to the frequency calibration error.
The loose time synchronization requirement TL states that the authenticity of the navigation message received at time t is guaranteed if |ΔT(t)|≤TL, at every t during the holdover period.
Finally, we can relate accuracy and misalignment using the bound
which allows us to upper bound the clock misalignment at any time t in terms of the frequency accuracy along the whole interval elapsed from the last calibration time t0.
Accuracy Loss for Receiver Clocks
Thanks to their affordable price and wide temperature operating conditions, quartz crystal oscillators are used for clock generation in GNSS receivers (see TABLE 1). We distinguish among simple, temperature-controlled crystal oscillators (TCXOs) and oven-controlled crystal oscillators (OCXOs). GNSS receivers typically employ TXCOs because they offer the best trade-off in terms of power consumption, price and typical accuracy.
Sources of Frequency Accuracy Loss. Quartz crystals are piezoelectric materials, therefore any additional stresses and environmental changes generate an additional voltage, decreasing the clock stability. In the automotive scenario, the main sources of accuracy loss are temperature changes, long-term aging, and the residual calibration frequency offset, while the impact of accelerations, vibrations, gravity variation and supply voltage oscillation can safely be neglected as they result in changes of a few parts per billion.
Currently, no analytic relationship is known between frequency accuracy and temperature for TCXOs (or OCXOs). Therefore, as reported in datasheets, the inaccuracy induced by the temperature changes is bounded by a constant value Ytemp across the whole operating temperature range. This yields a bound on the clock misalignment that increases linearly with the time from the last calibration.
Long-term aging has significant impacts on the clock frequency accuracy and may affect the device even when it is not used for a long time (see Figure 1). A critical aspect of this effect is that it is time-variant, with the accuracy loss increasing over time.
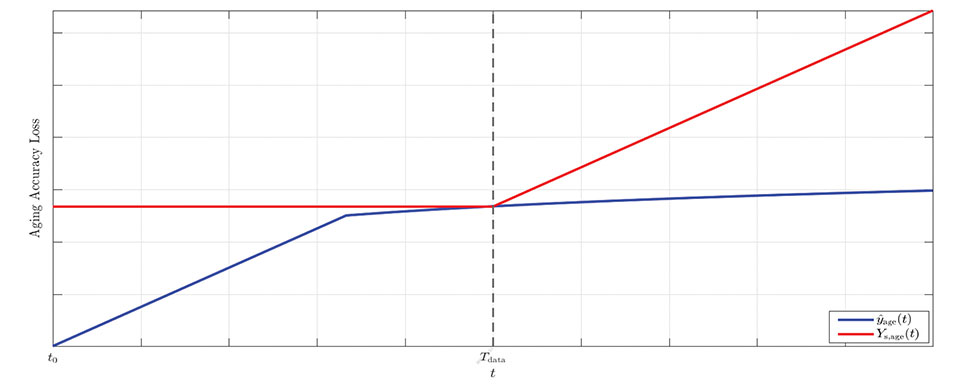
Figure 1. Graphical representation of the model for aging accuracy loss: upper-bound (red) versus estimated model (blue). (Image: R. Filler and J. Vig)
However, datasheets typically report a single value, Yage (Tdata ), which bounds the accuracy at a fixed time Tdata.
The effect of long-term aging for both TCXOs and OCXOs was investigated in a 1993 study by R. Filler and J. Vig measuring the accuracies of oscillator models for several years. The study concluded that a logarithmic fit is better suited for long-term measurements, while a linear fit is better suited for initial measurements (t<30 days) and is a loose upper-bound for longer times. Because we are interested in establishing a prudential upper bound rather than a precise estimate, we use the constant upper bound Yage (Tdata) for all t<Tdata and a linear upper bound for t>Tdata. This leads to a linearly increasing bound on the time offset before Tdata, and a quadratically increasing bound after Tdata.
Finally, the misalignment due to the frequency calibration error accumulates over time. An off-the-shelf oscillator has an initial accuracy that depends on the frequency tolerance ftol. To improve this, a precise calibration is performed, trying to synchronize the RTC with the nominal frequency f0, such as by using PTP. The contribution to the accuracy loss given by calibration can be bounded by Ycalib, a value set a priori either by system design or during the calibration process itself, yielding again a linearly increasing bound on the clock misalignment.
Bound on the Total Misalignment. In general, the cross-correlation between the uncertainties is unknown; we can only consider the worst-case scenario where the total uncertainty is bounded by the sum of the single bounds. This choice represents a prudential and conservative approach that may yield a rather loose bound with very high probability.
Thus, considering that all terms in the clock error bound increase over time, we can bound the total misalignment as
Example Values from Datasheet Specifications
Based on the above result, we can deem a commercial oscillator suitable for OSNMA operation if B(TR )≤TL. We can then compare the requirements for different RTCs, focusing on TCXOs designed for GNSS receivers suitable for the automotive scenario, with f0=52 MHz and a target operating temperature range between –20° Celsius and +85° Celsius. We assume that devices are subject to a calibration process, such that YcalibYtemp; thus we have neglected the calibration accuracy loss. We report in Table 2 the values of the misalignment bound, B(TR ), for TR=2 years and the maximum reset period TR,max such that B(TR,max)≤TL, with a loose time synchronization requirement TL=165s, as computed form the specs found in the datasheets.
Conclusions
To ensure the authenticity of the GNSS navigation message, the Galileo OSNMA protocol requires a loose synchronization between the transmitter and the receiver. The misalignment between transmitter and receiver clock needs to be lower than a threshold TL for the whole holdover period TR. In this article, we have investigated the causes of the misalignment and frequency deviation in clock generators commonly found on the market and defined a general relationship between TL ,TR and the specifications commonly found in datasheets. Finally, we examined several mass-market temperature-controlled crystal oscillator datasheets, evaluating their performance in terms of worst-case offset bound B(TR).
The bound represents a prudential conservative approach and may be rather loose. However, given the lack of a consistent statistical model, this is a reasonable solution. We conclude that most devices can satisfy the constraint B(TR)≤TL=165 s with a workshop reset period of TR = 2 years.
Acknowledgements
This study was conceived within the PATROL (Position Authenticated Tachograph foR OSNMA Launch) project, funded by the EU Agency for the Space Programme through the Fundamental Elements programme, under procurement No. GSA/OP/23/16 “Development, supply and testing of a Galileo open service authentication user terminal (OSNMA) for the GSA.”
The authors acknowledge the invaluable support provided by the PATROL technical team: Davide Marcantonio (Qascom), Fabio Pisoni, Giovanni Gogliettino and Domenico di Grazia (ST Microelectronics), Alexandre Allien and Francois Riou (FDC), Jacques Kunegel (ACTIA), Simón Cancela Díaz and Belén Villanueva Coello (GMV).
PATROL success was fostered by the commitment and support of Flavio Sbardellati (EUSPA Project Officer), Gonzalo Seco Granados and Alexander Rügamer (EUSPA external reviewers), Javier Simon (EUSPA reviewer), Ignacio Fernandez-Hernandez and Giovanni Vecchione (EC reviewers). The authors thank colleagues Giada Giorgi (UNIPD) and Lorenzo Dal Corso (Qascom) for reviewing this work.
The content of this publication does not reflect the official opinion of the European Union or of the EU Agency for the Space Programme. Responsibility for the information and views expressed therein lies entirely with the authors.
Francesco Ardizzon is a Ph.D. student and Nicola Laurenti an associate professor in the Department of Information Engineering of the University of Padova, Italy. Carlo Sarto is the head of the security engineering division and Giovanni Gamba the head of the SIGINT and EW division at Qascom S.r.l., in Bassano del Grappa, Italy.
REFERENCES
A. Perrig, R. Canetti, J. Tygar, and D. Song, “The TESLA broadcast authentication protocol,” RSA CryptoBytes, vol. 5, 11 2002.
I. Fernandez-Hernandez, T. Walter, A. Neish, and C. O’Driscoll, “Independent time synchronization for resilient GNSS receivers,” in 2020 International Technical Meeting of The Institute of Navigation, 02 2020, pp. 964–978.
I. Fernandez-Hernandez, V. Rijmen, G. Seco-Granados, J. Simon, I. Rodriguez, and J. D. Calle, “A Navigation Message Authentication proposal for the Galileo Open Service,” NAVIGATION, vol. 63, no. 1, pp. 85–102, 2016. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/navi.125
L. Cucchi, S. Damy, M. Paonni, M. Nicola, M. Troglia Gamba, B. Motella, and I. Fernandez-Hernandez, “Assessing galileo OSNMA under different user environments by means of a multi-purpose test bench, including a software-defined GNSS receiver,” in 4th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), 9 2021.
PATROL, https://www.patrol-osnma.eu/, last access 11 2021.
“IEEE standard definitions of physical quantities for fundamental frequency and time metrology—random instabilities,” IEEE Std 1139-2008, pp. c1–35, 2009.
J. Vig, “Quartz crystal resonators and oscillators for frequency control and timing applications – a tutorial,” in IEEE International Frequency Control Symposium Tutorials, 2016.
M. Lombardi, “Fundamentals of time and frequency,” in The Mechatronics Handbook, CRC Press, 01 2002, ch. 17.
J. Cartright, “Aging performance on crystals,” http://www.conwin.com/pdfs/aging perf crystals.pdf, 2008.
R. Filler and J. Vig, “Long-term aging of oscillators,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 40, no. 4, pp. 387–394, 1993.
W. Riley and D. Howe, Handbook of Frequency and Stability Analysis. Special Publication (NIST SP), National Institute of Standards and Technology, Gaithersburg, MD, 2008-07-01 00:07:00 2008.
“Performance specification: oscillator, crystal controlled, general specification for,” MIL-PRF-55310F, 2018.
“Fundamentals of quartz oscillators, application note 200-2,” http://leapsecond.com/hpan/an200-2.pdf, last access November 2021.
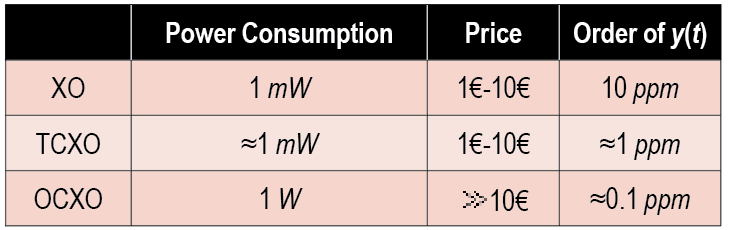
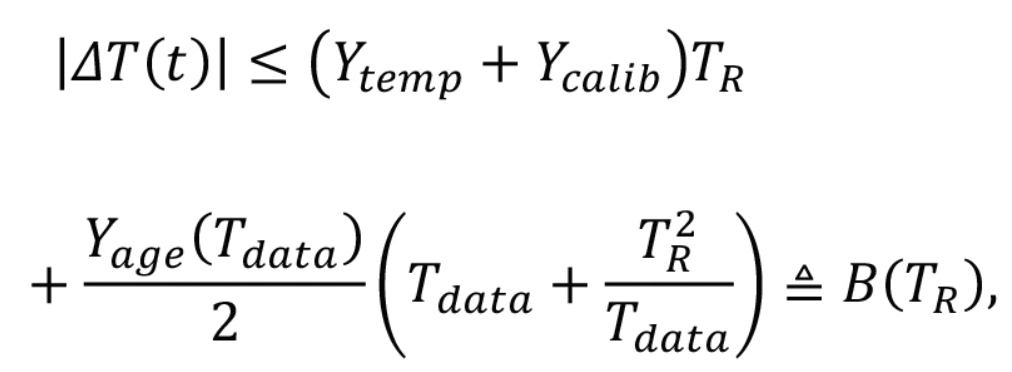
 Table 2. Bound values B(TR) and TR,max computed using several RTCs’ datasheet specs with TL=165 s and TR=2 years.
Table 2. Bound values B(TR) and TR,max computed using several RTCs’ datasheet specs with TL=165 s and TR=2 years.